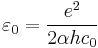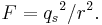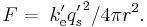Vacuum permittivity

The constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant, relates the units for electric charge to mechanical quantities such as length and force.[1] For example, the force between two separated electric charges (in vacuum) is given by Coulomb's law:

\ F_C = \frac{1} {4 \pi \varepsilon_0} \frac{q_1 q_2} {r^2}

where q1 and q2 are the charges, and r is the distance between them. Likewise, ε0 appears in Maxwell's equations, which describe the properties of electric and magnetic fields and electromagnetic radiation, and relate them to their sources.

The value of ε0 is defined in the International System of Units by the formula

\varepsilon_0 =\frac {1}{\mu_0 c_0^2} = 8.854187817...×10−12 A·s/(V·m) = 8.854187817...×10−12 F/m

where c0 is the speed of light in vacuum and μ0 is the magnetic constant or vacuum permeability.[2]

Contents

Value

The value of ε0 is defined by the formula

\varepsilon_0 =\frac {1}{\mu_0 c_0^2}

where c0 is the speed of light in vacuum,[3] and μ0 is the parameter that international Standards Organizations call the "magnetic constant" (commonly called vacuum permeability). Since μ0 has the defined value 4π × 10−7 H m−1,[4] and c0 has the defined value 299792458 m·s−1,[5] it follows that ε0 has a defined value given approximately by

ε0 ≈ 8.854187817... × 10−12 F·m−1 (or A2·s4·kg−1·m−3 in SI base units, or C2·N−1·m−2 or C·V−1·m−1 using other SI coherent units).[2][6]

The ellipsis (...) does not indicate experimental uncertainty, but the arbitrary termination of a nonrecurring decimal. The historical origins of the electric constant ε0, and its value, are explained in more detail below.

Under the proposals to redefine the ampere as a fixed number of elementary charges per second,[7] the electric constant would no longer have an exact fixed value. Instead, it would be defined by the equation

\varepsilon_0 =\frac {e^2}{2\alpha h c_0}

where e is the elementary charge, α is the fine structure constant and h is the Planck constant. The relative uncertainty in the value would be the same as that of the fine structure constant, currently 6.8 × 10−10.[2]

Terminology

Historically, the parameter ε0 has been known by many different names. The terms "vacuum permittivity" or its variants, such as "permittivity in/of vacuum",[8][9] "permittivity of empty space",[10] or "permittivity of free space"[11] are widespread. Standards Organizations worldwide now use "electric constant" as a uniform term for this quantity,[2] and official standards documents have adopted the term (although they continue to list the older terms as synonyms).[12][13]

Another historical synonym was "dielectric constant of vacuum", as "dielectric constant" was sometimes used in the past for the absolute permittivity.[14][15] However, in modern usage "dielectric constant" typically refers exclusively to a relative permittivity ε/ε0 and even this usage is considered "obsolete" by some standards bodies in favor of relative static permittivity.[13][16] Hence, the term "dielectric constant of vacuum" for the electric constant ε0 is considered obsolete by most modern authors, although occasional examples of continuing usage can be found.

As for notation, the constant can be denoted by either 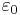\varepsilon_0\, or \epsilon_0\,, using either of the common glyphs for the letter epsilon.

Historical origin of the parameter ε0

As indicated above, the parameter ε0 is a measurement-system constant. Its presence in the equations now used to define electromagnetic quantities is the result of the so-called "rationalization" process described below. But the method of allocating a value to it is a consequence of the result that Maxwell's equations predict that, in free space, electromagnetic waves move with the speed of light. Understanding why ε0 has the value it does requires a brief understanding of the history of how electromagnetic measurement systems developed.

Rationalization of units

The experiments of Coulomb and others showed that the force F between two equal point-like "amounts" of electricity, situated a distance r apart in free space, should be given by a formula that has the form

F = \; k_{\mathrm{e}} Q^2/r^2,

where Q is a quantity that represents the amount of electricity present at each of the two points, and ke is a constant. If one is starting with no constraints, then the value of ke may be chosen arbitrarily.[17] For each different choice of ke there is a different "interpretation" of Q: to avoid confusion, each different "interpretation" has to be allocated a distinctive name and symbol.

In one of the systems of equations and units agreed in the late 1800s, called the "centimetre-gram-second electrostatic system of units" (the cgs esu system), the constant ke was taken equal to 1, and a quantity now called "gaussian electric charge" qs was defined by the resulting equation

F = {q_s}^2/r^2.

The unit of gaussian charge, the statcoulomb, is such that two units, a distance of 1 centimetre apart, repel each other with a force equal to the cgs unit of force, the dyne. Thus the unit of gaussian charge can also be written 1 dyne1/2 cm. "Gaussian electric charge" is not the same mathematical quantity as modern (rmks) electric charge and is not measured in coulombs.

The idea subsequently developed that it would be better, in situations of spherical geometry, to include a factor 4π in equations like Coulomb's law, and write it in the form:

F = \; k'_{\mathrm{e}} {q'_s}^2/4 \pi r^2.

This idea is called "rationalization". The quantities q's and ke' are not the same as those in the older convention. Putting ke'=1 generates a unit of electricity of different size, but it still has the same dimensions as the cgs esu system.

The next step was to treat the quantity representing "amount of electricity" as a fundamental quantity in its own right, denoted by the symbol q, and to write Coulomb's Law in its modern form:

\ F = q^2/4 \pi \epsilon_0 r^2.

The system of equations thus generated is known as the rationalized metre-kilogram-second (rmks) equation system, or "metre-kilogram-second-ampere (mksa)" equation system. This is system used to define the SI units.[18] The new quantity q is given the name "rmks electric charge", or (nowadays) just "electric charge". Clearly, the quantity qs used in the old cgs esu system is related to the new quantity q by

\ q_s = q/(4\pi\epsilon_0)^{1/2}.

Determination of a value for ε0

One now adds the requirement that one wants force to be measured in newtons, distance in metres, and charge to be measured in the engineers' practical unit, the coulomb, which is defined as the charge accumulated when a current of 1 ampere flows for one second. This shows that the parameter ε0 should be allocated the unit C2·N−1·m−2 (or equivalent units - in practice "farads per metre").

In order to establish the numerical value of ε0, one makes use of the fact that if one uses the rationalized forms of Coulomb's law and Ampère's force law (and other ideas) to develop Maxwell's equations, then the relationship stated above is found to exist between ε0, μ0 and c0. In principle, one has a choice of deciding whether to make the coulomb or the ampere the fundamental unit of electricity and magnetism. The decision was taken internationally to use the ampere. This means that the value of ε0 is determined by the values of c0 and μ0, as stated above. For a brief explanation of how the value of μ0 is decided, see the article about μ0.

Permittivity of real media

By convention, the electric constant ε0 appears in the relationship that defines the electric displacement field D in terms of the electric field E. In real media this relationship has the form

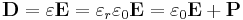\mathbf{D} = \varepsilon \mathbf{E} = \varepsilon_r \varepsilon_0 \mathbf{E} = \varepsilon_0 \mathbf{E} + \mathbf{P},

where ε is the permittivity, εr the relative static permittivity, and P is the classical electrical polarization density of the medium. In vacuum, the polarization P = 0.

See also

Notes

  1. ↑ "electric constant". Electropedia: International Electrotechnical Vocabulary (IEC 60050). Geneva: International Electrotechnical Commission. http://www.electropedia.org/iev/iev.nsf/display?openform&ievref=121-11-03. Retrieved 2010-04-02 .
  2. ↑ 2.0 2.1 2.2 2.3 Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Rev. Mod. Phys. 80: 633–730. doi:10.1103/RevModPhys.80.633. http://physics.nist.gov/cuu/Constants/codata.pdf.  Direct link to value..
  3. ↑ Quote from NIST: "Current practice is to use c0 to denote the speed of light in vacuum according to ISO 31. In the original Recommendation of 1983, the symbol c was used for this purpose." See NIST Special Publication 330, Appendix 2, p. 45
  4. ↑ See the last sentence of the NIST definition of ampere.
  5. ↑ See the last sentence of the NIST definition of meter.
  6. ↑ A summary of the definitions of c0, μ0 and ε0 is provided in the 2006 CODATA Report: CODATA report, pp. 6-7
  7. ↑ "Recommendation E1". Report of the 25th meeting (15–16 March 2007), Consultative Committee for Electricity and Magnetism (CCEM). Sèvres, France: International Bureau for Weights and Measures. http://www.bipm.org/utils/common/pdf/CCEM25.pdf .
  8. ↑ SM Sze & Ng KK (2007). "Appendix E". Physics of semiconductor devices (Third ed.). New York: Wiley-Interscience. p. 788. ISBN 0-471-14323-5. http://worldcat.org/isbn/0-471-14323-5. 
  9. ↑ RS Muller, Kamins TI & Chan M (2003). Device electronics for integrated circuits (Third ed.). New York: Wiley. Inside front cover. ISBN 0-471-59398-2. http://worldcat.org/isbn/0-471-59398-2. 
  10. ↑ FW Sears, Zemansky MW & Young HD (1985). College physics. Reading, Mass.: Addison-Wesley. p. 40. ISBN 0201078368. http://books.google.com/?id=AvVQAAAAMAAJ&q=zemansky+%22permittivity+of+empty+space%22&dq=zemansky+%22permittivity+of+empty+space%22. 
  11. ↑ B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics (Wiley, 1991)
  12. ↑ International Bureau of Weights and Measures (2006). "The International System of Units (SI)" (PDF). p. 12. http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf. 
  13. ↑ 13.0 13.1 Braslavsky, S.E. (2007). "Glossary of terms used in photochemistry (IUPAC recommendations 2006)". Pure and Applied Chemistry 79: 293–465; see p. 348.. doi:10.1351/pac200779030293. http://www.iupac.org/publications/pac/2007/pdf/7903x0293.pdf 
  14. ↑ "Naturkonstanten". Freie Universität Berlin. http://www.chemie.fu-berlin.de/chemistry/general/constants.html. 
  15. ↑ King, Ronold W. P. (1963). Fundamental Electromagnetic Theory. New York: Dover. p. 139. 
  16. ↑ IEEE Standards Board (1997). "IEEE Standard Definitions of Terms for Radio Wave Propagation". p. 6. http://ieeexplore.ieee.org/iel4/5697/15269/00705931.pdf?arnumber=705931. 
  17. ↑ For an introduction to the subject of choices for independent units, see John David Jackson (1999). "Appendix on units and dimensions". Classical electrodynamics (Third ed.). New York: Wiley. pp. 775 et seq... ISBN 047130932X. http://worldcat.org/isbn/047130932X. 
  18. ↑ International Bureau of Weights and Measures. "The International System of Units (SI) and the corresponding system of quantities". http://www.bipm.org/en/si/si_brochure/chapter1/1-2.html.